Interpolated table lookups using SSE2 [1/2]
Something that you are very likely to encounter, when writing SSE2 assembler is the issue of using tables for looking up data. While this is a very simple operation in C, it presents a challenge with a lot of pitfalls, when using SSE2.
When to use lookup tables?
In general, avoid them, if it is within the possibility. Let’s have a look at a simple example:
const float ushort_to_float[65535];
float convert_unsigned_short_to_float(unsigned short value) {
return ushort_to_float[value];
}
This is quite tempting in C – especially if you can do some transformations on the value, by modifying the lookup table, if you need something expensive like the square root, use the inverted value. But lets look at the drawbacks.
The table is 256KB, so you will run out of level 1 cache on most CPUs. In C the penalty for a value in L1 cache this is usually a couple of cycles per value, but if it has to be fetched from L2, we are talking about 15 cycles or more on most platforms. But if it saves you a division and a square root or something similar the trade-off may be ok for you.
In SSE2, the trade-off picture is changed. Here the penalty per pixel for doing the lookup remains the same (or even rises), while calculating the value is usually only about 25% of cost of what the C-code. So you can see – we can do a lot more calculations in SSE2 before using a table should even be considered.
What if I have to use lookup tables?
There might be cases, where using tables are the only way, because calculating the values simply aren’t practically possible in SSE2. A practical example of this from Rawstudio is the curve correction, that involves mapping input values to output values based on an n-point 2D curve.
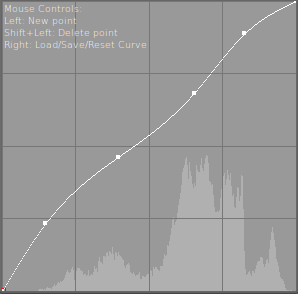
Curve Correction: Nearly impossible without using lookup tables.
In the “old days”, we used a table with 65535 16 bit entries, that simply gave the output value, much as the example above. The table was 128KB, so again, we had a lot of L1 cache misses.
When we re-wrote colour correction, everything internally was converted to float, which made the table 256KB, and even slower. Furthermore it also made sure that we lost a lot of the float precision, by having to fit the float values into 65535 slots.
So we got two problems:
- Bad precision
- Table too large for L1 cache
Using lookup tables for float data
Since most of these lookups are fairly linear, without too sudden peaks, usually we are fairly in the clear if we reduce the precision of the table, and do linear interpolation between them instead. This avoids posterizing the image data, because all float values will have a unique output. Here is an example, where we use a curve correction with only 256 input/output values, and interpolate them instead.
float curve_samples[257];
// Make sure we have an extra entry, so we avoid an
// "if (lookup > 255)" later.
curve_samples[256] = curve_samples[255];
for (all pixels...) {
// Look up and interpolate
float lookup = CLAMP(input * 256.0f, 0.0f, 255.9999f);
float v0 = curve_samples[(int)lookup];
float v1 = curve_samples[(int)lookup + 1];
lookup -= floorf(lookup);
output = v0 * (1.0f - lookup) + v1 * lookup;
}
So now the table is only 1KB in size and fits very nicely within the Level 1 cache. This approach solves both our problems, but at the expense of some calculations. Whether 256 entries are enough is up for you to decide, but the principle applies for all sizes. The “floor” function can be quite slow on some compilers/CPUs, but it is here to demonstrate the algorithm. We will touch this later.
In part two, I will look at the actual implementation – there are still a lot of pitfalls in making this work in real life.
PS. If you enjoy technical stuff like this, please leave a comment.
I can’t say I know too much about the technical details of image processing, but I do appreciate the insight post like these give. Thanks!
It seems like you could reduce the size further is you used a different data type for the LUT, for instance a 16-bit or 8-bit int. With my monitor at 1024 pixels high, I couldn’t imagine being able to enter a curve at more than 10-bits precision, and that’s if the screen is maximized. Sounds like the image data is in float, but does it take too many cycles to cast an int to a float? I wonder if the loss of precision would be noticable. Anyways, these are just questions floating in my head, and I’m not trying to criticize your implementation, you folks know way more than I ever will about this stuff.
The game is a little different when you are dealing with Raw data, because you operate in a linear colorspace. Because of this you need additional precision, since errors become very visible in dark areas.
See this PDF on why you need at least 16 bit precision for Raw images:
http://www.adobe.com/products/photoshop/pdfs/linear_gamma.pdf
Yes, I enjoyed this posting very much. Thanks!
Thanks, I enjoy this kind of blog posts! Keep them coming :)
[…] Continued from part 1… […]
The problem with that approach is that decreasing the table precision leads to at least two problems.
First, the curve downscaler 65536->256 has to be chosen carefully.
And then such a big downscale can’t be reasonably inversed using a simple linear interpolation w/o introducing aliasing problems.
Do you have some PSNR numbers comparing the original results using interpolation between the 65536 sampling points of the curve, and the faster 256 entry table interpolation ?
Hi Edouard!
>First, the curve downscaler 65536->256 has to be chosen carefully.
The curve isn’t downscaled as such – the curve is simply sampled with 256 entries instead of 65536. So we get 256 exact values, and not some that are derived from 65536.
>And then such a big downscale can’t be reasonably inversed using a simple linear interpolation w/o introducing aliasing problems.
How do you get to that result? The curve is an input->output mapping, where neutral is input=output (straight line). You would have to have a curve that has variations where the correction is changed at a 1/128th pixel resolution, which simply wouldn’t make sense.
So unless you have information with a frequency close to or above the nyquist frequency, a linear interpolation should not generate aliasing.
If you consider the image of the curve, you have approximately the horizontal resolution of the image (the image is ~290 pixels wide). The vertical sample point have float point precision, so the vertical resolution is very precise. The vertical resolution is the reason there is no precision issues, even with such small tables.
>Do you have some PSNR numbers comparing the original results using interpolation between the 65536 sampling points of the curve, and the faster 256 entry table interpolation ?
I’ll make a few calculations that calculates the min, max and average error on “realistic” and some “extreme” curves.